结构的动力学分析可分为线性动力学分析和瞬态动力学分析，瞬态动力学通常涉及较强的非线性和时间相关的载荷，仿真工程师往往需要花费大量的时间调试模型才能得到合理的结果。而线性动力学不考虑模型中的非线性和时间相关的载荷，因此计算效率相对于瞬态动力学较高，被广泛用于工程分析中。常用的线性动力学分析有模态分析、谐响应分析、随机振动分析、反应谱分析和基于模态的瞬态动力学分析。

谐响应分析又称为扫频分析，用于计算线性系统在不同频率的正弦周期载荷下的响应，其不考虑载荷作用在结构一瞬间的瞬态响应。通过谐响应分析可以获得线性系统在特定载荷下特征频率附近对应的响应并通过云图识别结构的薄弱部位，同时也可得到结构在整个扫频分析中的响应。本期为大家介绍OptFuture中的谐响应分析。

本次示例支架模型及边界条件如图1所示。在蓝色高亮处设置固定约束，用于模拟与外部法兰结构的螺栓连接；在两臂红色高亮圆孔处分别施加方向相反，大小为20N的力载荷。模型整体结构阻尼为0.05，材料弹性模量200GPa，泊松比0.3，密度7850kg/m^3。扫频范围1Hz~1000Hz，扫频点总数为100，这意味着软件将会以10Hz为扫频间隔，给出100个扫频结果。

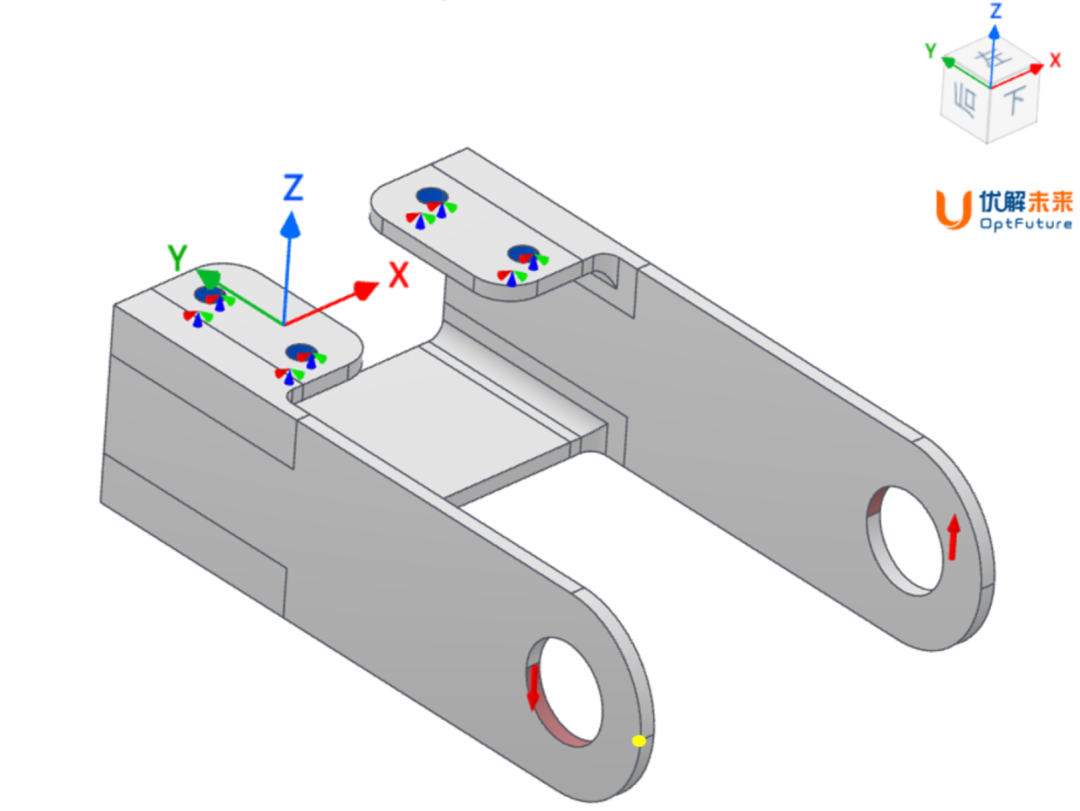
图1 支架模型及边界条件设置

使用国外商软计算该模型结果作为对标，图2为对标商软与OptFuture计算上述特定载荷下，扫频频率为1000Hz时的合位移结果。图中表明OptFuture在1000Hz合位移实部结果变形趋势与对标商软结果一致，对标商软合位移实部为8.2e-4mm，OptFuture合位移实部为8.38e-4mm，相对偏差仅为2.1%。

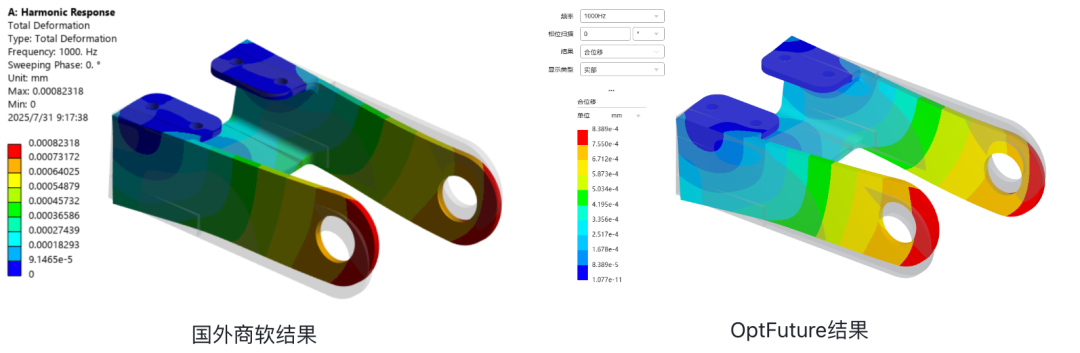
图2 1000Hz合位移实部结果

谐响应结果常通过频率-结果线图获取结构在扫频范围内的响应，这一功能通过OptFuture后处理中的线图即可实现。以图1支架中黄色高亮点为关注对象（下文简称为探针点），绘制“频率-Z向位移”结果曲线，图3给出了对标商软和OptFuture绘制探针点Z向位移实部和虚部随频率的变化曲线。从图中可以看出OptFuture计算结果趋势与对标商软基本一致，结果均在300Hz和370Hz频率点出现响应峰值。

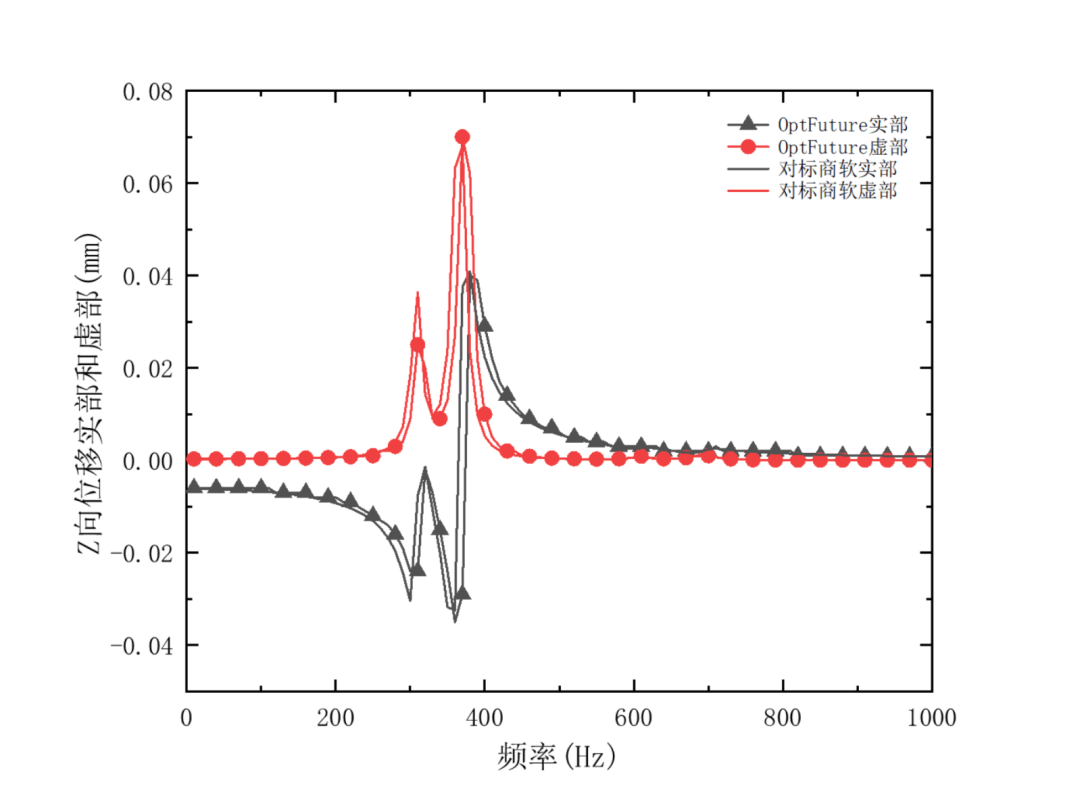
图3  OptFuture与国外商软Z向位移实部和虚部结果对比

图4为对标商软和OptFuture绘制探针点Z向位移幅值和相位随频率变化趋势，从图中看出OptFuture计算结果趋势与对标商软基本一致。Z向位移幅值的峰值同样在300Hz和370Hz附近，由于该算例存在多个载荷，且模型存在阻尼，探针点位移的相位随频率发生变化。

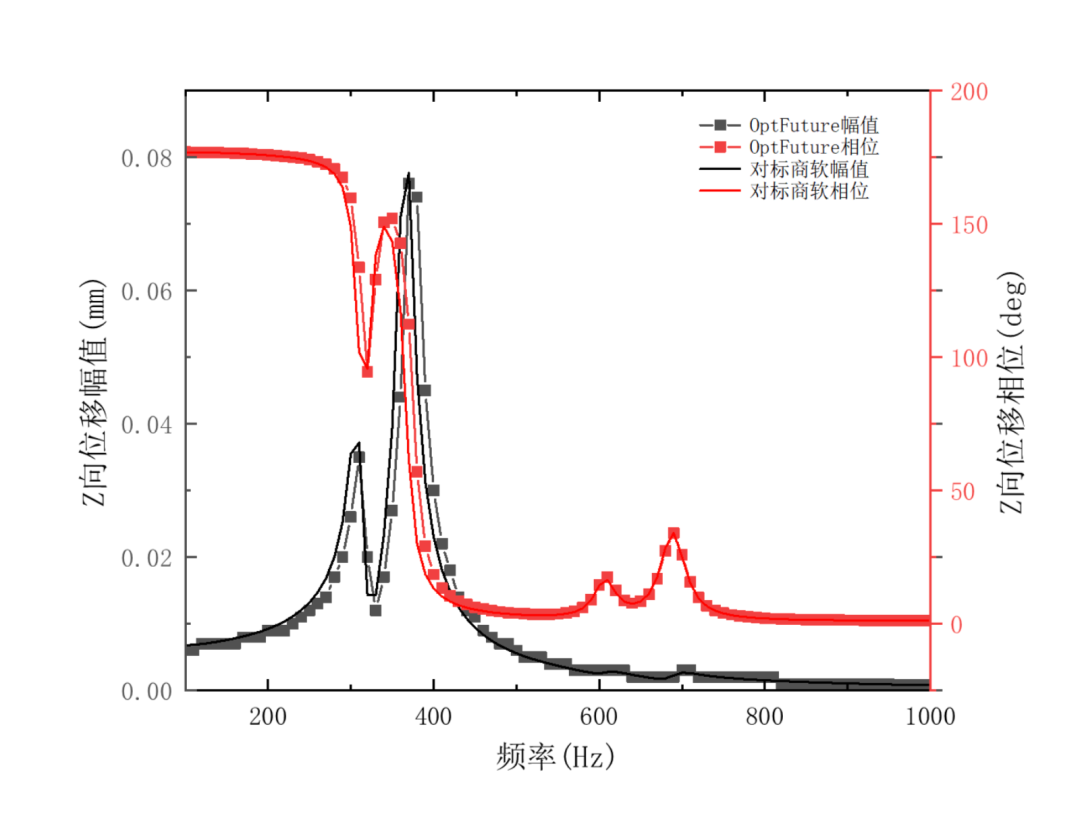
图4 OptFuture与国外商软Z向位移幅值和相位结果对比

接下来我们使用OptFuture谐响应的模态叠加法计算此算例。需要注意的是，在使用模态叠加法前，需要创建模态分析作为前置分析模块。为了保证模态叠加法的求解精度，模态分析所计算的模态频率要涵盖谐响应分析所关注的整个扫频范围。由于篇幅限制，表1仅给出了对标商软和OptFuture计算该支架在上述约束状态下的前6阶模态结果，结果显示各阶模态振型基本一致，频率最大偏差仅0.48%。

表1 约束模态计算结果

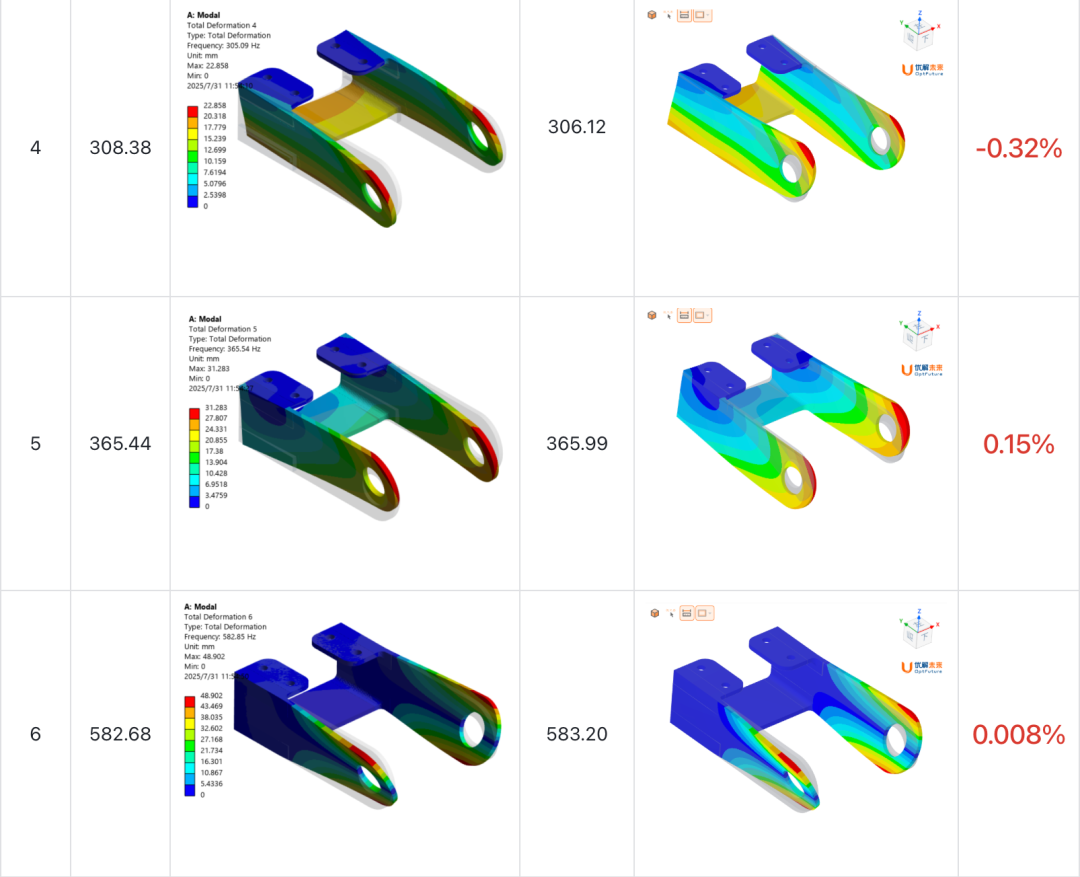
图5为分别使用直接法和模态叠加法计算探针点Z向位移实部和虚部对比，由于直接法直接求解动力学方程，所以理论上直接法鲁棒性比模态叠加法更好，图中显示两种方法的结果趋势基本一致。结合图5与表1中模态的结果，可以发现谐响应的Z向位移峰值发生在第4阶和第5阶频率，且模态振型方向同样为Z向。

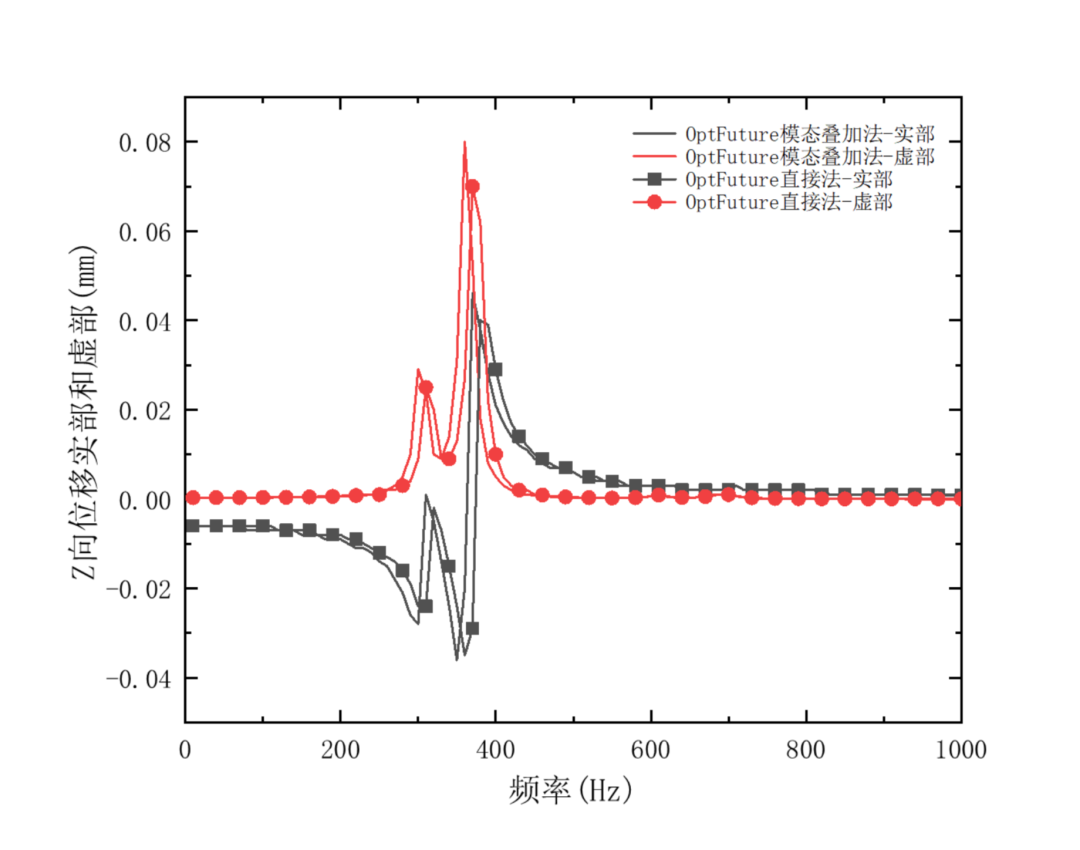
图5 OptFuture直接法与模态叠加法结果对比

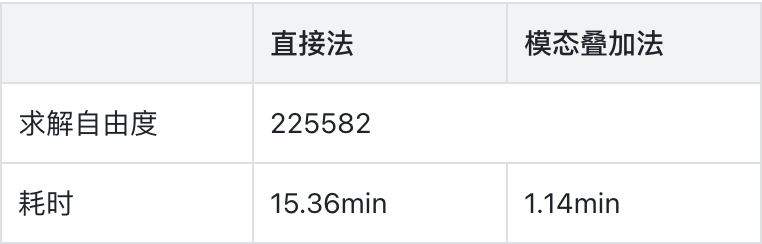
表2中对比了两种求解方法在求解自由度一致情况下的计算效率，通过对比可知模态叠加法的求解效率远高于直接法，且模态叠加法的结果趋势基本与直接法一致。因此在大型结构的谐响应分析中，往往推荐采用模态叠加法以加快求解速度，提升求解效率。

表2 谐响应直接法与模态叠加法计算效率对比

本次为大家介绍了OptFuture中的谐响应功能应用示例，感兴趣的读者朋友可以直接进入我们的官网注册账号进行软件试用，往期文章内所提到的模型参数以及OptFuture模型，可以通过我们的官方公众号或者客服微信群（见文末二维码）索取。

客服微信